Thursday, July 16, 2015

Circuits connected in Series

 In a series circuit the current is the same for all elements and corresponding voltage is different.
                                            I = I_1 = I_2 = \dots = I_n
 Then expression for series component of resistor capacitor and inductor are given by

Resistor:
            The total resistance of resistors in series is equal to the sum of their individual resistances:

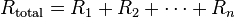
 R_\mathrm{total} = R_1 + R_2 + \cdots + R_n
                                     
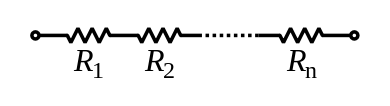
                          This is a diagram of several resistors, connected end to end, with the same amount of current through each.
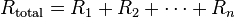
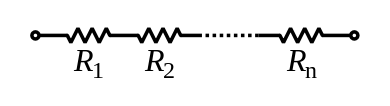
Electrical conductance presents a reciprocal quantity to resistance. Total conductance of a series circuits of pure resistors, therefore, can be calculated from the following expression:
\frac{1}{G_\mathrm{total}} = \frac{1}{G_1} + \frac{1}{G_2} + \cdots + \frac{1}{G_n}.
For a special case of two resistors in series, the total conductance is equal to:
G_{total} = \frac{G_1 G_2}{G_1+G_2}.
Inductor:
             In that the total inductance of non-coupled inductors in series is equal to the sum of their individual inductances:
A diagram of several inductors, connected end to end, with the same amount of current going through each.
L_\mathrm{total} = L_1 + L_2 + \cdots + L_n
 it is difficult to prevent adjacent inductors from influencing each other, as the magnetic field of one device couples with the windings of its neighbours. This influence is defined by the mutual inductance M.
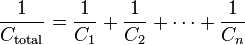 For three coils, there are six mutual inductances M_{12}, M_{13}, M_{23} and M_{21}, M_{31} and M_{32}. There are also the three self-inductances of the three coils: M_{11}, M_{22} and M_{33}.
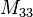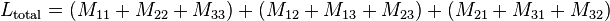ThereforeL_\mathrm{total} = (M_{11} + M_{22} + M_{33}) + (M_{12} + M_{13} + M_{23}) + (M_{21} + M_{31} + M_{32})

By reciprocity M_{ij} = M_{ji}
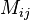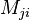Capacitor:
           
 The total capacitance of capacitors in series is equal to the reciprocal of the sum of the reciprocals of their individual capacitances:
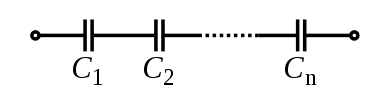
A diagram of several capacitors, connected end to end, with the same amount of current going through each.
\frac{1}{C_\mathrm{total}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n}.

Posted by at
Labels:

1 comment:

  1. UnknownMarch 11, 2022 at 11:14 PM

    I definitely enjoying every little bit of it and I have you bookmarked to check out new stuff you post. 100kv capacitors

    ReplyDelete

Subscribe to: Post Comments (Atom)