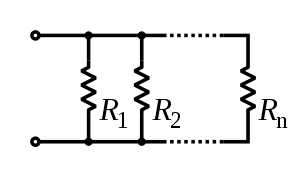
In a parallel circuit the voltage is the same for all elements and corresponding current is different.

hen expression for series component of resistor capacitor and inductor are given by
Resistors:
The current in each individual resistor is found by Ohm's law. Factoring out the voltage gives
 .
.
To find the total resistance of all components, add the reciprocals of the resistances  of each component and take the reciprocal of the sum. Total resistance will always be less than the value of the smallest resistance:
of each component and take the reciprocal of the sum. Total resistance will always be less than the value of the smallest resistance:
 of each component and take the reciprocal of the sum. Total resistance will always be less than the value of the smallest resistance:
of each component and take the reciprocal of the sum. Total resistance will always be less than the value of the smallest resistance: .
.
For only two resistors, the unreciprocated expression is reasonably simple:
To find the current in a component with resistance  , use Ohm's law again:
, use Ohm's law again:
 , use Ohm's law again:
, use Ohm's law again: .
.
The components divide the current according to their reciprocal resistances, so, in the case of two resistors,
 .
.
electrical conductance  is reciprocal to resistance, the expression for total conductance of a parallel circuit of resistors reads:
is reciprocal to resistance, the expression for total conductance of a parallel circuit of resistors reads:
 is reciprocal to resistance, the expression for total conductance of a parallel circuit of resistors reads:
is reciprocal to resistance, the expression for total conductance of a parallel circuit of resistors reads: .
.
Inductors:
Inductors follow the same law, in that the total inductance of non-coupled inductors in parallel is equal to the reciprocal of the sum of the reciprocals of their individual inductances:
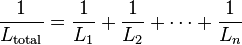 .
.
If the inductors are situated in each other's magnetic fields, this approach is invalid due to mutual inductance. If the mutual inductance between two coils in parallel is M, the equivalent inductor is:
If 
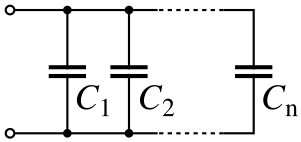
Capacitors:
The total capacitance of capacitors in parallel is equal to the sum of their individual capacitances:
 .
.




No comments:
Post a Comment