1. common Emitter amplifier
2. common Base amplifier
3. common Collector amplifier
COMMON-COLLECTOR CONFIGURATION
Since there is no phase reversal between the input and output
circuits of a common-collector configuration, the feedback network does not need to provide a phase
shift. However, since the voltage gain is less than unity and the power gain is low, the common-collector
configuration is very seldom used in oscillator circuits.
COMMON-BASE CONFIGURATION
The power gain and voltage gain of the common-base
configuration are high enough to give satisfactory operation in an oscillator circuit. The wide range between
the input resistance and the output resistance make impedance matching slightly harder to achieve in the
common-base circuit than in the common-emitter circuit. An advantage of the common-base configuration is
that it exhibits better high-frequency response than does the common-emitter configuration.
COMMON-EMITTER CONFIGURATION
The common-emitter configuration has high power gain and is
used in low-frequency applications.For the energy which is fed back from the output to be in phase with the
energy at the input, the feedback network of a common-emitter oscillator must provide a phase shift of
approximately 180 degrees.


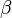
















 .
. of each component and take the reciprocal of the sum. Total resistance will always be less than the value of the smallest resistance:
of each component and take the reciprocal of the sum. Total resistance will always be less than the value of the smallest resistance: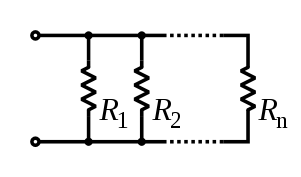
 .
.
 .
. .
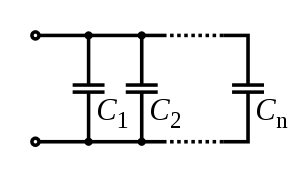
. is reciprocal to resistance, the expression for total conductance of a parallel circuit of resistors reads:
is reciprocal to resistance, the expression for total conductance of a parallel circuit of resistors reads: .
.
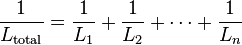 .
.
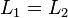

 .
.
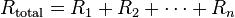
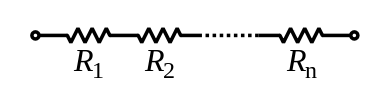
 .
.


 ,
,  ,
,  and
and  ,
,  and
and  . There are also the three self-inductances of the three coils:
. There are also the three self-inductances of the three coils:  ,
,  and
and 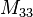 .
.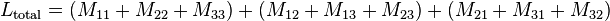
 =
= 
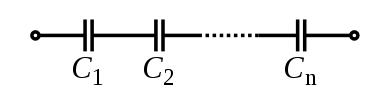
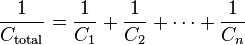 .
.